What Are The 3 Values We Get After Using K Fold Cross Validation In Machine Learning

How to Configure k-Fold Cross-Validation

Terminal Updated on August 26, 2020

The k-fold cantankerous-validation procedure is a standard method for estimating the performance of a motorcar learning algorithm on a dataset.

A common value for chiliad is 10, although how do nosotros know that this configuration is appropriate for our dataset and our algorithms?

1 approach is to explore the outcome of different k values on the estimate of model performance and compare this to an ideal examination condition. This can help to choose an appropriate value for thousand.

Once a k-value is called, it can be used to evaluate a suite of different algorithms on the dataset and the distribution of results tin can be compared to an evaluation of the same algorithms using an ideal examination condition to see if they are highly correlated or non. If correlated, it confirms the chosen configuration is a robust approximation for the platonic test condition.

In this tutorial, you will observe how to configure and evaluate configurations of chiliad-fold cross-validation.

After completing this tutorial, you will know:

• How to evaluate a automobile learning algorithm using k-fold cross-validation on a dataset.
• How to perform a sensitivity analysis of thousand-values for k-fold cross-validation.
• How to summate the correlation between a cross-validation test harness and an ideal examination status.

Kick-beginning your project with my new book Machine Learning Mastery With Python, including step-by-step tutorials and the Python source code files for all examples.

Permit'south get started.

How to Configure yard-Fold Cantankerous-Validation
Photo by Patricia Farrell, some rights reserved.

Tutorial Overview

This tutorial is divided into 3 parts; they are:

1. k-Fold Cross-Validation
2. Sensitivity Analysis for k
3. Correlation of Test Harness With Target

grand-Fold Cross-Validation

It is common to evaluate machine learning models on a dataset using m-fold cross-validation.

The chiliad-fold cantankerous-validation procedure divides a limited dataset into k non-overlapping folds. Each of the m folds is given an opportunity to be used as a held-back test fix, whilst all other folds collectively are used as a preparation dataset. A total of k models are fit and evaluated on the yard hold-out test sets and the mean performance is reported.

For more on the k-fold cross-validation procedure, run into the tutorial:

• A Gentle Introduction to thousand-fold Cantankerous-Validation

The yard-fold cross-validation process tin be implemented easily using the scikit-learn motorcar learning library.

First, let'south define a constructed nomenclature dataset that we can employ as the basis of this tutorial.

The make_classification() role tin be used to create a synthetic binary classification dataset. We volition configure it to generate 100 samples each with 20 input features, 15 of which contribute to the target variable.

The case below creates and summarizes the dataset.

# exam classification dataset from sklearn . datasets import brand _nomenclature # ascertain dataset X , y = make_classification ( n_samples = 100 , n_features = xx , n_informative = xv , n_redundant = 5 , random_state = ane ) # summarize the dataset print ( X . shape , y . shape )

Running the example creates the dataset and confirms that it contains 100 samples and 10 input variables.

The fixed seed for the pseudorandom number generator ensures that we become the same samples each fourth dimension the dataset is generated.

Side by side, nosotros can evaluate a model on this dataset using k-fold cantankerous-validation.

We will evaluate a LogisticRegression model and utilize the KFold class to perform the cantankerous-validation, configured to shuffle the dataset and ready k=10, a popular default.

The cross_val_score() function will be used to perform the evaluation, taking the dataset and cantankerous-validation configuration and returning a listing of scores calculated for each fold.

The complete example is listed below.

1 2 3 4 5 half-dozen seven 8 ix 10 11 12 xiii 14 fifteen sixteen 17

# evaluate a logistic regression model using k-fold cross-validation from numpy import mean from numpy import std from sklearn . datasets import make_classification from sklearn . model_selection import KFold from sklearn . model_selection import cross_val_score from sklearn . linear_model import LogisticRegression # create dataset X , y = make_classification ( n_samples = 100 , n_features = 20 , n_informative = 15 , n_redundant = 5 , random_state = 1 ) # set the cross-validation process cv = KFold ( n_splits = ten , random_state = 1 , shuffle = True ) # create model model = LogisticRegression ( ) # evaluate model scores = cross_val_score ( model , X , y , scoring = 'accuracy' , cv = cv , n_jobs = - 1 ) # report operation impress ( 'Accuracy: %.3f (%.3f)' % ( mean ( scores ) , std ( scores ) ) )

Running the example creates the dataset, then evaluates a logistic regression model on it using 10-fold cross-validation. The hateful nomenclature accuracy on the dataset is then reported.

Notation: Your results may vary given the stochastic nature of the algorithm or evaluation process, or differences in numerical precision. Consider running the instance a few times and compare the average result.

In this example, we can see that the model achieved an estimated classification accurateness of about 85.0 per centum.

Now that we are familiar with k-fold cantankerous-validation, let's wait at how we might configure the process.

Sensitivity Analysis for yard

The key configuration parameter for thou-fold cantankerous-validation is m that defines the number folds in which to split up a given dataset.

Common values are m=3, 1000=five, and m=x, and by far the well-nigh popular value used in applied machine learning to evaluate models is k=x. The reason for this is studies were performed and k=10 was constitute to provide expert trade-off of low computational price and low bias in an estimate of model performance.

How practise nosotros know what value of k to use when evaluating models on our own dataset?

You lot can choose k=10, but how do you know this makes sense for your dataset?

I approach to answering this question is to perform a sensitivity analysis for different grand values. That is, evaluate the functioning of the same model on the aforementioned dataset with different values of k and see how they compare.

The expectation is that low values of k will upshot in a noisy estimate of model functioning and big values of g volition result in a less noisy estimate of model performance.

Simply noisy compared to what?

We don't know the truthful performance of the model when making predictions on new/unseen data, as we don't have access to new/unseen information. If we did, nosotros would make employ of it in the evaluation of the model.

Nevertheless, nosotros can choose a exam condition that represents an "ideal" or every bit-best-as-we-can-attain "ideal" estimate of model performance.

I arroyo would be to train the model on all bachelor data and guess the functioning on a separate large and representative hold-out dataset. The performance on this hold-out dataset would represent the "true" operation of the model and any cross-validation performances on the training dataset would represent an approximate of this score.

This is rarely possible as nosotros frequently do not have enough data to agree some dorsum and use it as a test gear up. Kaggle motorcar learning competitions are one exception to this, where we practise accept a hold-out test set, a sample of which is evaluated via submissions.

Instead, nosotros can simulate this case using the leave-one-out cross-validation (LOOCV), a computationally expensive version of cantankerous-validation where grand=N, and N is the total number of examples in the grooming dataset. That is, each sample in the training ready is given an case to be used lone as the test evaluation dataset. It is rarely used for large datasets as information technology is computationally expensive, although it can provide a good judge of model performance given the available information.

We can then compare the mean classification accuracy for different k values to the mean classification accuracy from LOOCV on the same dataset. The difference between the scores provides a rough proxy for how well a thousand value approximates the ideal model evaluation test condition.

Let'south explore how to implement a sensitivity analysis of k-fold cross-validation.

Offset, let's define a function to create the dataset. This allows you to change the dataset to your own if you want.

# create the dataset def get_dataset ( n_samples = 100 ) : X , y = make_classification ( n_samples = n_samples , n_features = xx , n_informative = xv , n_redundant = five , random_state = ane ) return X , y

Next, we tin can define a dataset to create the model to evaluate.

Over again, this separation allows you lot to change the model to your ain if you want.

# remember the model to be evaluate def get_model ( ) : model = LogisticRegression ( ) return model

Adjacent, yous can define a function to evaluate the model on the dataset given a test condition. The test condition could be an instance of the KFold configured with a given m-value, or it could exist an instance of LeaveOneOut that represents our ideal test status.

The function returns the hateful classification accuracy every bit well as the min and max accuracy from the folds. We can use the min and max to summarize the distribution of scores.

# evaluate the model using a given exam status def evaluate_model ( cv ) : # get the dataset 10 , y = get_dataset ( ) # go the model model = get_model ( ) # evaluate the model scores = cross_val_score ( model , X , y , scoring = 'accurateness' , cv = cv , n_jobs = - 1 ) # render scores render mean ( scores ) , scores . min ( ) , scores . max ( )

Adjacent, we can summate the model functioning using the LOOCV procedure.

. . . # calculate the platonic test condition ideal , _ , _ = evaluate_model ( LeaveOneOut ( ) ) impress ( 'Ideal: %.3f' % ideal )

We can then ascertain the grand values to evaluate. In this case, we will test values between 2 and 30.

. . . # define folds to test folds = range ( ii , 31 )

We can then evaluate each value in plow and store the results equally nosotros become.

. . . # record hateful and min/max of each prepare of results ways , mins , maxs = list ( ) , list ( ) , listing ( ) # evaluate each thousand value for g in folds : # define the test condition cv = KFold ( n_splits = k , shuffle = Truthful , random_state = 1 ) # evaluate k value k_mean , k_min , k_max = evaluate_model ( cv ) # written report operation print ( '> folds=%d, accuracy=%.3f (%.3f,%.3f)' % ( k , k_mean , k_min , k_max ) ) # store mean accurateness means . append ( k_mean ) # store min and max relative to the hateful mins . append ( k_mean - k_min ) maxs . suspend ( k_max - k_mean )

Finally, we tin can plot the results for estimation.

. . . # line plot of one thousand mean values with min/max mistake bars pyplot . errorbar ( folds , means , yerr = [ mins , maxs ] , fmt = 'o' ) # plot the platonic instance in a dissever color pyplot . plot ( folds , [ ideal for _ in range ( len ( folds ) ) ] , color = 'r' ) # show the plot pyplot . show ( )

Tying this together, the complete case is listed below.

i 2 3 4 5 half-dozen 7 viii 9 10 11 12 13 14 15 16 17 18 19 twenty 21 22 23 24 25 26 27 28 29 thirty 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 l 51 52 53 54 55 56

# sensitivity analysis of k in m-fold cantankerous-validation from numpy import mean from sklearn . datasets import make_classification from sklearn . model_selection import LeaveOneOut from sklearn . model_selection import KFold from sklearn . model_selection import cross_val_score from sklearn . linear_model import LogisticRegression from matplotlib import pyplot # create the dataset def get_dataset ( n_samples = 100 ) : X , y = make_classification ( n_samples = n_samples , n_features = twenty , n_informative = 15 , n_redundant = 5 , random_state = 1 ) render X , y # retrieve the model to be evaluate def get_model ( ) : model = LogisticRegression ( ) render model # evaluate the model using a given test condition def evaluate_model ( cv ) : # become the dataset 10 , y = get_dataset ( ) # get the model model = get_model ( ) # evaluate the model scores = cross_val_score ( model , Ten , y , scoring = 'accuracy' , cv = cv , n_jobs = - one ) # render scores render mean ( scores ) , scores . min ( ) , scores . max ( ) # calculate the platonic test condition ideal , _ , _ = evaluate_model ( LeaveOneOut ( ) ) impress ( 'Platonic: %.3f' % ideal ) # ascertain folds to examination folds = range ( 2 , 31 ) # tape mean and min/max of each fix of results ways , mins , maxs = list ( ) , listing ( ) , list ( ) # evaluate each g value for chiliad in folds : # ascertain the test status cv = KFold ( n_splits = g , shuffle = Truthful , random_state = 1 ) # evaluate m value k_mean , k_min , k_max = evaluate_model ( cv ) # study performance print ( '> folds=%d, accuracy=%.3f (%.3f,%.3f)' % ( k , k_mean , k_min , k_max ) ) # shop mean accuracy means . suspend ( k_mean ) # store min and max relative to the mean mins . append ( k_mean - k_min ) maxs . suspend ( k_max - k_mean ) # line plot of k mean values with min/max error bars pyplot . errorbar ( folds , means , yerr = [ mins , maxs ] , fmt = 'o' ) # plot the platonic case in a divide colour pyplot . plot ( folds , [ ideal for _ in range ( len ( folds ) ) ] , color = 'r' ) # show the plot pyplot . show ( )

Running the example first reports the LOOCV, and so the mean, min, and max accuracy for each k value that was evaluated.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the instance a few times and compare the average outcome.

In this example, we tin see that the LOOCV result was most 84 percent, slightly lower than the k=10 result of 85 pct.

i 2 3 4 five half dozen seven 8 nine 10 11 12 thirteen 14 xv sixteen 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Ideal: 0.840 > folds=2, accuracy=0.740 (0.700,0.780) > folds=iii, accuracy=0.749 (0.697,0.824) > folds=4, accurateness=0.790 (0.640,0.920) > folds=5, accuracy=0.810 (0.600,0.950) > folds=six, accuracy=0.820 (0.688,0.941) > folds=7, accurateness=0.799 (0.571,1.000) > folds=viii, accuracy=0.811 (0.385,0.923) > folds=9, accurateness=0.829 (0.636,ane.000) > folds=x, accuracy=0.850 (0.600,i.000) > folds=11, accuracy=0.829 (0.667,1.000) > folds=12, accuracy=0.785 (0.250,1.000) > folds=thirteen, accuracy=0.839 (0.571,1.000) > folds=14, accuracy=0.807 (0.429,1.000) > folds=15, accuracy=0.821 (0.571,1.000) > folds=xvi, accurateness=0.827 (0.500,ane.000) > folds=17, accuracy=0.816 (0.600,i.000) > folds=18, accuracy=0.831 (0.600,1.000) > folds=19, accuracy=0.826 (0.600,1.000) > folds=xx, accurateness=0.830 (0.600,1.000) > folds=21, accuracy=0.814 (0.500,1.000) > folds=22, accurateness=0.820 (0.500,i.000) > folds=23, accuracy=0.802 (0.250,1.000) > folds=24, accuracy=0.804 (0.250,1.000) > folds=25, accuracy=0.810 (0.250,1.000) > folds=26, accuracy=0.804 (0.250,1.000) > folds=27, accuracy=0.818 (0.250,1.000) > folds=28, accuracy=0.821 (0.250,1.000) > folds=29, accurateness=0.822 (0.250,i.000) > folds=30, accuracy=0.822 (0.333,ane.000)

A line plot is created comparison the mean accuracy scores to the LOOCV event with the min and max of each result distribution indicated using error bars.

The results propose that for this model on this dataset, most thou values underestimate the operation of the model compared to the ideal case. The results suggest that perhaps k=10 alone is slightly optimistic and perhaps yard=13 might be a more accurate estimate.

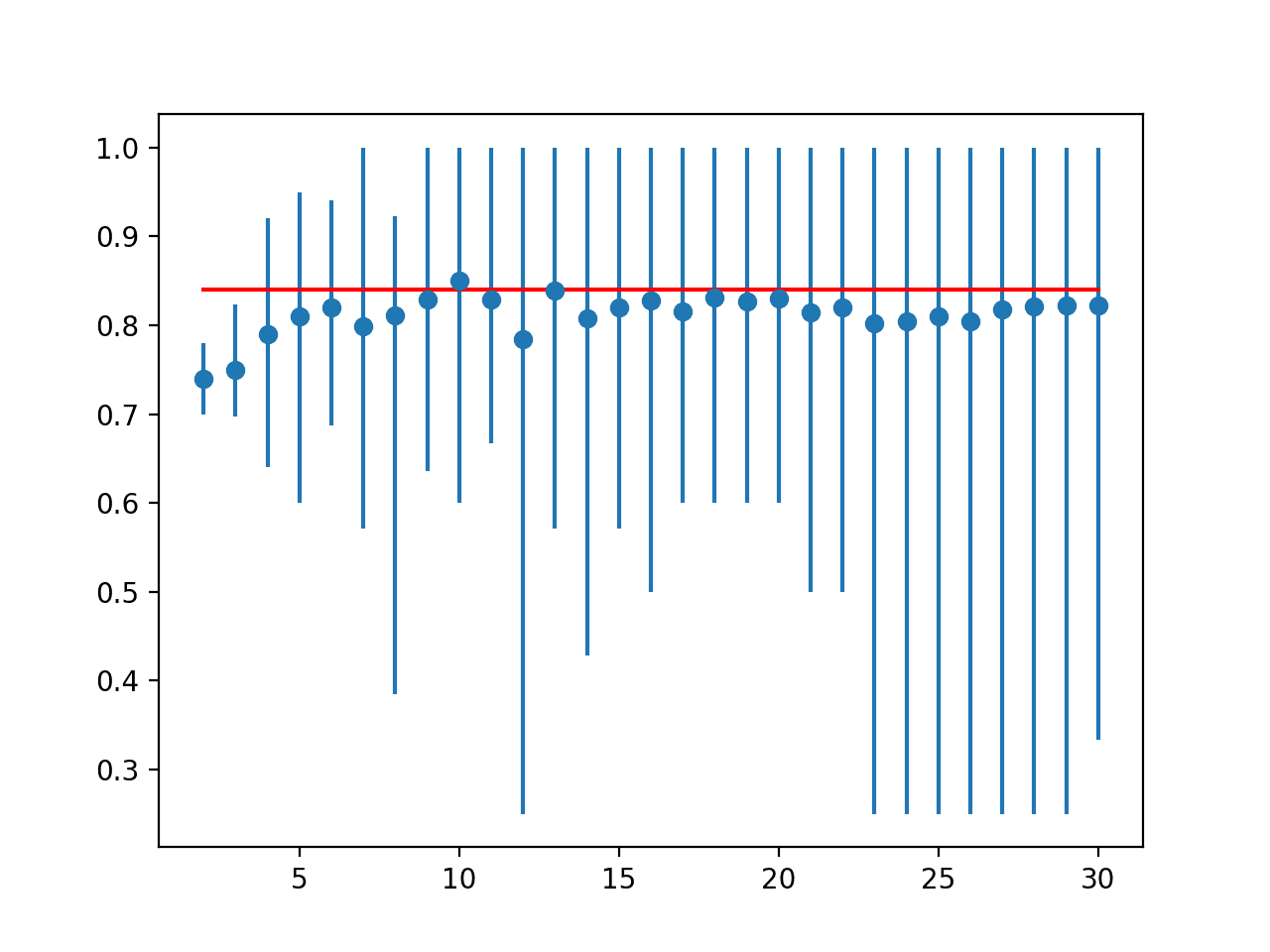
Line Plot of Mean Accuracy for Cantankerous-Validation k-Values With Error Bars (Blue) vs. the Ideal Case (red)

This provides a template that you can use to perform a sensitivity analysis of k values of your chosen model on your dataset against a given platonic exam condition.

Correlation of Test Harness With Target

Once a exam harness is chosen, another consideration is how well it matches the platonic exam condition across unlike algorithms.

It is possible that for some algorithms and some configurations, the k-fold cross-validation will be a amend approximation of the ideal test condition compared to other algorithms and algorithm configurations.

Nosotros tin evaluate and report on this relationship explicitly. This can be achieved by calculating how well the m-fold cantankerous-validation results across a range of algorithms match the evaluation of the same algorithms on the ideal test condition.

The Pearson'south correlation coefficient can be calculated betwixt the 2 groups of scores to measure how closely they lucifer. That is, do they modify together in the aforementioned ways: when 1 algorithm looks meliorate than another via k-fold cantankerous-validation, does this hold on the platonic test condition?

We expect to see a potent positive correlation between the scores, such every bit 0.5 or higher. A low correlation suggests the need to change the thou-fold cross-validation test harness to better match the ideal exam condition.

Outset, we can ascertain a function that volition create a listing of standard machine learning models to evaluate via each examination harness.

1 2 3 iv 5 6 7 eight 9 10 11 12 13 xiv fifteen 16 17 eighteen 19 xx 21 22

# get a listing of models to evaluate def get_models ( ) : models = list ( ) models . append ( LogisticRegression ( ) ) models . append ( RidgeClassifier ( ) ) models . suspend ( SGDClassifier ( ) ) models . append ( PassiveAggressiveClassifier ( ) ) models . append ( KNeighborsClassifier ( ) ) models . append ( DecisionTreeClassifier ( ) ) models . append ( ExtraTreeClassifier ( ) ) models . append ( LinearSVC ( ) ) models . append ( SVC ( ) ) models . append ( GaussianNB ( ) ) models . suspend ( AdaBoostClassifier ( ) ) models . append ( BaggingClassifier ( ) ) models . append ( RandomForestClassifier ( ) ) models . suspend ( ExtraTreesClassifier ( ) ) models . append ( GaussianProcessClassifier ( ) ) models . suspend ( GradientBoostingClassifier ( ) ) models . append ( LinearDiscriminantAnalysis ( ) ) models . append ( QuadraticDiscriminantAnalysis ( ) ) return models

Nosotros will use k=x for the called test harness.

We can then enumerate each model and evaluate it using x-fold cross-validation and our ideal test condition, in this instance, LOOCV.

ane 2 3 four 5 half-dozen seven eight nine ten 11 12 13 14 15 16 17 xviii 19 20 21

. . . # define exam weather ideal_cv = LeaveOneOut ( ) cv = KFold ( n_splits = 10 , shuffle = True , random_state = i ) # become the list of models to consider models = get_models ( ) # collect results ideal_results , cv_results = list ( ) , listing ( ) # evaluate each model for model in models : # evaluate model using each examination status cv_mean = evaluate_model ( cv , model ) ideal_mean = evaluate_model ( ideal_cv , model ) # cheque for invalid results if isnan ( cv_mean ) or isnan ( ideal_mean ) : continue # shop results cv_results . append ( cv_mean ) ideal_results . append ( ideal_mean ) # summarize progress print ( '>%s: ideal=%.3f, cv=%.3f' % ( type ( model ) . __name__ , ideal_mean , cv_mean ) )

We can and then calculate the correlation between the mean classification accuracy from the x-fold cross-validation examination harness and the LOOCV test harness.

. . . # calculate the correlation between each test condition corr , _ = pearsonr ( cv_results , ideal_results ) impress ( 'Correlation: %.3f' % corr )

Finally, nosotros tin create a besprinkle plot of the two sets of results and describe a line of best fit to visually see how well they change together.

. . . # besprinkle plot of results pyplot . scatter ( cv_results , ideal_results ) # plot the line of best fit coeff , bias = polyfit ( cv_results , ideal_results , 1 ) line = coeff * asarray ( cv_results ) + bias pyplot . plot ( cv_results , line , color = 'r' ) # show the plot pyplot . show ( )

Tying all of this together, the consummate case is listed below.

1 2 3 4 5 six 7 8 9 10 11 12 13 fourteen 15 sixteen 17 18 nineteen 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 seventy 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102

# correlation between test harness and platonic exam condition from numpy import hateful from numpy import isnan from numpy import asarray from numpy import polyfit from scipy . stats import pearsonr from matplotlib import pyplot from sklearn . datasets import make_classification from sklearn . model_selection import KFold from sklearn . model_selection import LeaveOneOut from sklearn . model_selection import cross_val_score from sklearn . linear_model import LogisticRegression from sklearn . linear_model import RidgeClassifier from sklearn . linear_model import SGDClassifier from sklearn . linear_model import PassiveAggressiveClassifier from sklearn . neighbors import KNeighborsClassifier from sklearn . tree import DecisionTreeClassifier from sklearn . tree import ExtraTreeClassifier from sklearn . svm import LinearSVC from sklearn . svm import SVC from sklearn . naive_bayes import GaussianNB from sklearn . ensemble import AdaBoostClassifier from sklearn . ensemble import BaggingClassifier from sklearn . ensemble import RandomForestClassifier from sklearn . ensemble import ExtraTreesClassifier from sklearn . gaussian_process import GaussianProcessClassifier from sklearn . ensemble import GradientBoostingClassifier from sklearn . discriminant_analysis import LinearDiscriminantAnalysis from sklearn . discriminant_analysis import QuadraticDiscriminantAnalysis # create the dataset def get_dataset ( n_samples = 100 ) : X , y = make_classification ( n_samples = n_samples , n_features = 20 , n_informative = 15 , n_redundant = 5 , random_state = 1 ) return X , y # get a list of models to evaluate def get_models ( ) : models = listing ( ) models . suspend ( LogisticRegression ( ) ) models . suspend ( RidgeClassifier ( ) ) models . append ( SGDClassifier ( ) ) models . append ( PassiveAggressiveClassifier ( ) ) models . append ( KNeighborsClassifier ( ) ) models . append ( DecisionTreeClassifier ( ) ) models . append ( ExtraTreeClassifier ( ) ) models . append ( LinearSVC ( ) ) models . append ( SVC ( ) ) models . append ( GaussianNB ( ) ) models . append ( AdaBoostClassifier ( ) ) models . suspend ( BaggingClassifier ( ) ) models . append ( RandomForestClassifier ( ) ) models . append ( ExtraTreesClassifier ( ) ) models . append ( GaussianProcessClassifier ( ) ) models . suspend ( GradientBoostingClassifier ( ) ) models . suspend ( LinearDiscriminantAnalysis ( ) ) models . suspend ( QuadraticDiscriminantAnalysis ( ) ) return models # evaluate the model using a given test condition def evaluate_model ( cv , model ) : # get the dataset Ten , y = get_dataset ( ) # evaluate the model scores = cross_val_score ( model , X , y , scoring = 'accuracy' , cv = cv , n_jobs = - 1 ) # return scores return hateful ( scores ) # define test conditions ideal_cv = LeaveOneOut ( ) cv = KFold ( n_splits = 10 , shuffle = Truthful , random_state = ane ) # get the list of models to consider models = get_models ( ) # collect results ideal_results , cv_results = list ( ) , list ( ) # evaluate each model for model in models : # evaluate model using each exam condition cv_mean = evaluate_model ( cv , model ) ideal_mean = evaluate_model ( ideal_cv , model ) # bank check for invalid results if isnan ( cv_mean ) or isnan ( ideal_mean ) : go on # store results cv_results . suspend ( cv_mean ) ideal_results . suspend ( ideal_mean ) # summarize progress print ( '>%s: ideal=%.3f, cv=%.3f' % ( type ( model ) . __name__ , ideal_mean , cv_mean ) ) # calculate the correlation between each exam condition corr , _ = pearsonr ( cv_results , ideal_results ) print ( 'Correlation: %.3f' % corr ) # scatter plot of results pyplot . besprinkle ( cv_results , ideal_results ) # plot the line of all-time fit coeff , bias = polyfit ( cv_results , ideal_results , one ) line = coeff * asarray ( cv_results ) + bias pyplot . plot ( cv_results , line , color = 'r' ) # characterization the plot pyplot . title ( '10-fold CV vs LOOCV Mean Accuracy' ) pyplot . xlabel ( 'Mean Accuracy (10-fold CV)' ) pyplot . ylabel ( 'Hateful Accuracy (LOOCV)' ) # evidence the plot pyplot . show ( )

Running the example reports the mean nomenclature accuracy for each algorithm calculated via each test harness.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the boilerplate outcome.

Yous may see some warnings that you can safely ignore, such as:

We can run across that for some algorithms, the test harness over-estimates the accuracy compared to LOOCV, and in other cases, information technology nether-estimates the accuracy. This is to be expected.

At the end of the run, we tin see that the correlation between the two sets of results is reported. In this example, we can see that a correlation of 0.746 is reported, which is a skillful strong positive correlation. The results propose that 10-fold cross-validation does provide a good approximation for the LOOCV examination harness on this dataset as calculated with 18 popular machine learning algorithms.

1 2 3 4 5 vi 7 8 ix 10 11 12 13 14 15 sixteen 17 18 19

>LogisticRegression: ideal=0.840, cv=0.850 >RidgeClassifier: ideal=0.830, cv=0.830 >SGDClassifier: platonic=0.730, cv=0.790 >PassiveAggressiveClassifier: ideal=0.780, cv=0.760 >KNeighborsClassifier: ideal=0.760, cv=0.770 >DecisionTreeClassifier: ideal=0.690, cv=0.630 >ExtraTreeClassifier: ideal=0.710, cv=0.620 >LinearSVC: ideal=0.850, cv=0.830 >SVC: platonic=0.900, cv=0.880 >GaussianNB: platonic=0.730, cv=0.720 >AdaBoostClassifier: ideal=0.740, cv=0.740 >BaggingClassifier: ideal=0.770, cv=0.740 >RandomForestClassifier: ideal=0.810, cv=0.790 >ExtraTreesClassifier: ideal=0.820, cv=0.820 >GaussianProcessClassifier: ideal=0.790, cv=0.760 >GradientBoostingClassifier: ideal=0.820, cv=0.820 >LinearDiscriminantAnalysis: ideal=0.830, cv=0.830 >QuadraticDiscriminantAnalysis: platonic=0.610, cv=0.760 Correlation: 0.746

Finally, a besprinkle plot is created comparing the distribution of mean accuracy scores for the test harness (x-axis) vs. the accurateness scores via LOOCV (y-axis).

A red line of best fit is drawn through the results showing the strong linear correlation.

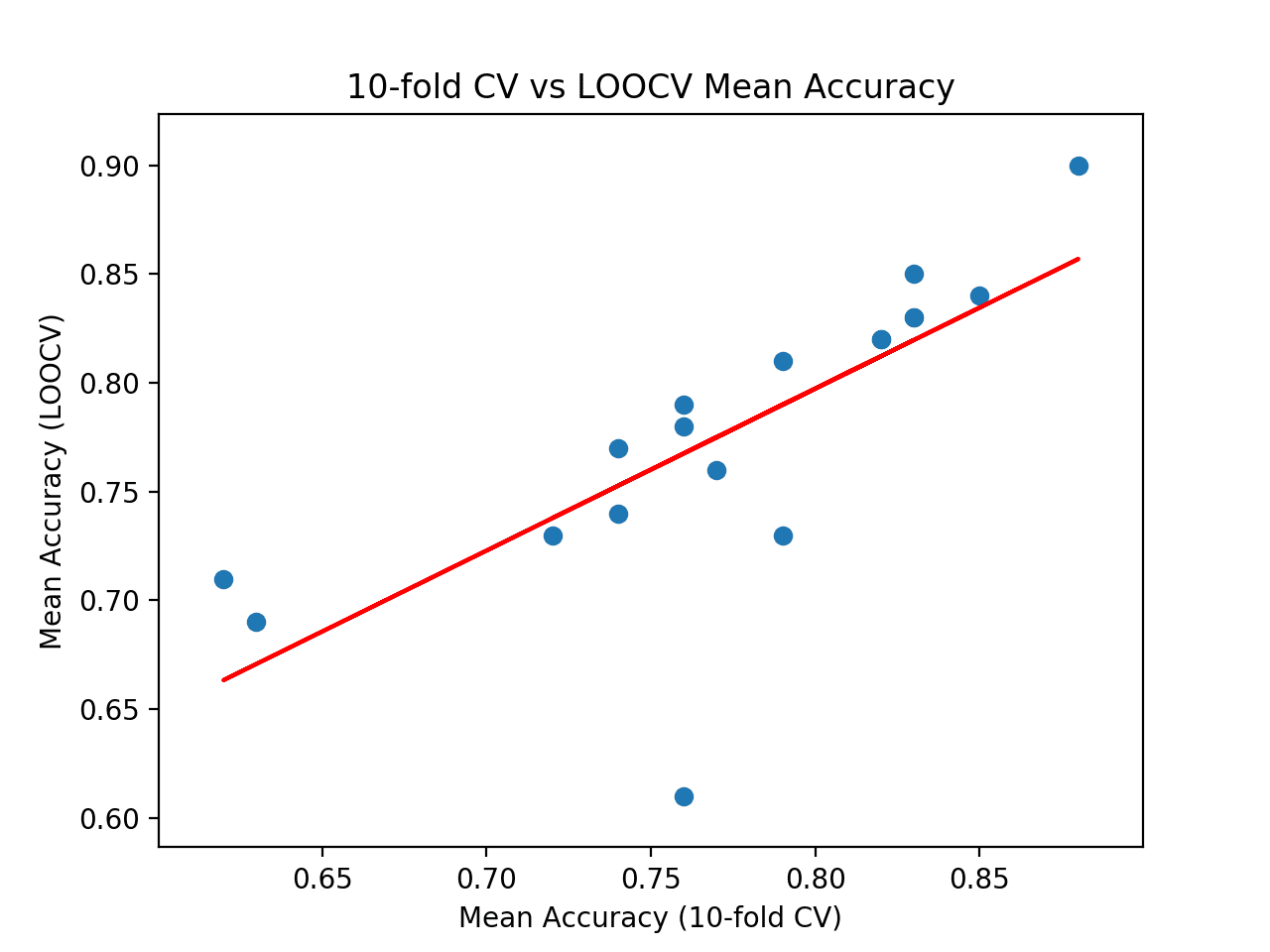
Besprinkle Plot of Cross-Validation vs. Ideal Test Mean Accurateness With Line of Best Fit

This provides a harness for comparing your chosen test harness to an ideal test condition on your own dataset.

Further Reading

This section provides more resources on the topic if yous are looking to get deeper.

Tutorials

• A Gentle Introduction to thou-fold Cross-Validation
• How to Set up k-Fold Cross-Validation for Imbalanced Classification

APIs

• sklearn.model_selection.KFold API.
• sklearn.model_selection.LeaveOneOut API.
• sklearn.model_selection.cross_val_score API.

Articles

• Cantankerous-validation (statistics), Wikipedia.

Summary

In this tutorial, you discovered how to configure and evaluate configurations of k-fold cross-validation.

Specifically, you learned:

• How to evaluate a car learning algorithm using k-fold cross-validation on a dataset.
• How to perform a sensitivity analysis of k-values for k-fold cross-validation.
• How to summate the correlation between a cross-validation test harness and an ideal examination status.

Exercise you have any questions?
Ask your questions in the comments beneath and I volition do my best to answer.

Find Fast Machine Learning in Python!

Develop Your Own Models in Minutes

...with just a few lines of scikit-acquire code

Learn how in my new Ebook:
Machine Learning Mastery With Python

Covers self-report tutorials and cease-to-terminate projects like:
Loading data, visualization, modeling, tuning, and much more...

Finally Bring Machine Learning To
Your Own Projects

Skip the Academics. Just Results.

See What's Within

Source: https://machinelearningmastery.com/how-to-configure-k-fold-cross-validation/

Posted by: lucktope2001.blogspot.com

Share this post